Spatial Enhancements
Introduction
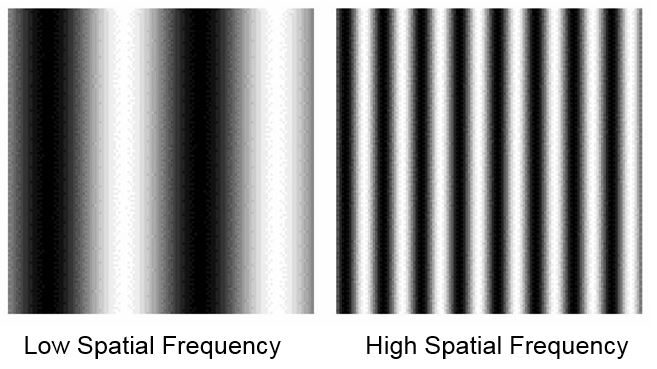
Spatial enhancement techniques use the concept of spatial frequency within an image. Spatial frequency is the manner in which gray-scale values change relative to their neighbors within an image. If there is a slow, gradual change in gray scale in an image from one side of the image to the other, the image is said to have a low spatial frequency. If pixel values vary radically for adjacent pixels in an image, the image is said to have a high spatial frequency.
Spatial Filtering
Spatial Filtering is done to emphasize or de-emphasize certain features depending on the spatial frequency. Spatial filters can be used to sharpen or emphasize the edges in an image or to smooth an image. Spatial filtering is a “local” operation, the pixel values in an original image are modified based on the values of the neighboring pixels
Convolution
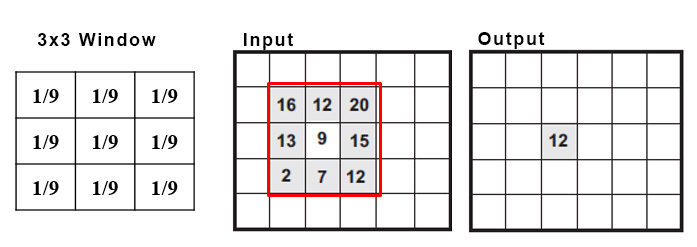
Convolution involves a moving window that contains an array of coefficients or weighted factors. The window is moved throughout the original image and the output pixel number at the center of the window is obtained by multiplying each coefficients by the pixel values of the surrounding pixels. The moving window is also referred to as a "Neighborhood" or "Kernel". The windows or kernels are usually defined by there size. For example a 3 X 3 window is made up of a matrix of 3 rows and 3 columns. A 5 x 5 window is larger with consisting of a matrix of 5 rows and 5 columns. The larger the window size, the "stronger" the filter.
In the below example a 3 X 3 pixel window is used to determine the new pixel value. In this example all pixels are evenly weighted (averaged) to produce the output pixel value. This is an example of a Low Pass Filter
Low Pass Filters
In effect the high and low values within each “neighborhood” will be averaged out, reducing extreme value in the data. Low pass filters are used for noise reduction and to reduce local variation.
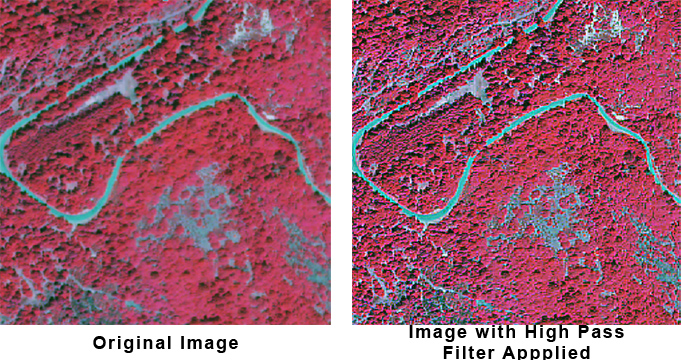
High Pass Filters
High-pass filters are designed to emphasize high frequency changes and de-emphasize more general, low frequency change. High pass filters are also known as sharpening filters and can bring out the boundaries between features (for example, where a water body meets the forest), thus sharpening edges between objects.
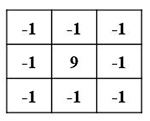3 X 3 High Pass filter. By giving negative weights to its neighbors, the filter accentuates the local detail by pulling out the differences or the boundaries between objects 