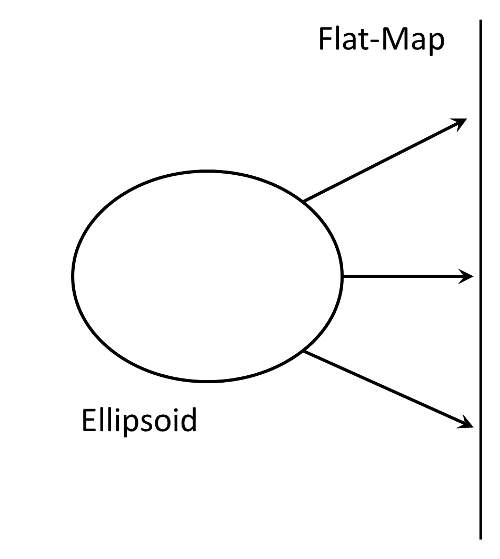
The world is a three dimensional (3D) ellipsoid but almost all the media we work with is 2 dimensional (2D). This means we must convert spherical coordinates on the earth to rectangular coordinates in a flat surface. This is the challenge of "projecting" data and it has been worked on for hundreds of years.
Before projecting data, we have to define a coordinate system for working on a 2D plane, also known as rectangular coordinates.

Rene' Descartes (Cartesius in Latin), developed the idea of rectangular coordinates and wrote about it in 1637.
In a rectangular coordinate system, we have two "axis" which intersect at a 90 degree angle. We can then have a value for "x" on the horizontal axis and "y" on the vertical axis that uniquely identifies each point within the system. You've seen this before from geometry.
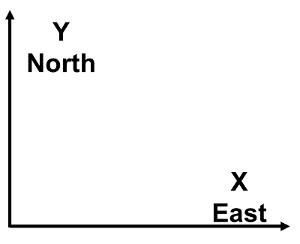
If we label the y value as a "northing" and an x value as an "easting", then we can identify anywhere in the system with a coordinate based on it's position toward the north and it's position toward the east. This is the basis for the coordinate system used when data has been "projected".
The earth is an ellipsoid. To view spatial data on paper and computer screens, we need to project the data onto a 2d surface. This is called "projecting".
© Copyright 2018 HSU - All rights reserved.