This lab will introduce you to modeling presence/absence data with GLMs. This is also the first full-modeling lab. A key element of this lab is examining the response of the data vs. the predicted output of the model and how both relate to the predictor variables.
Note: Remember to include the glm2 library in the code below.
The function below will create synthetic presence/absence data for evaluating GLMs. Copy it into R now and compile them.
############################################################################
# Creates a data frame with Xs ranging from 1 to the number of entries
# and "Measures" with 1/2 set to 0 and 1/2 set to 1. The lower have of
# the X values have measures at 0.
# ProportionRandom - amount of uniform randomness to add
############################################################################
Categories1D_Random=function(NumEntries=10,ProportionRandom=0.4)
{
Range=NumEntries*ProportionRandom/2
Ys=as.vector(array(1:NumEntries))
Xs=as.vector(array(1:NumEntries))
Measures=as.vector(array(1:NumEntries))
for (Index in 1:NumEntries)
{
Xs[Index]=Index #runif(1,0,100)
Ys[Index]=Index #runif(1,0,100)
Threshold=0.5
Random=0
if (ProportionRandom!=0) Random=runif(1,-Range,Range)
if (Xs[Index]>NumEntries/2+Random) Measures[Index]=1
else Measures[Index]=0
}
TheDataFrame = data.frame(Ys, Xs, Measures)
}
The code below will create a synthetic data set for a logistic model using the function above. Try it now in R. Note that the data contains some randomness to make the values overlap a bit.
TheData=Categories1D_Random(100) # create a set of binary data plot(TheData$Xs,TheData$Measures) # plot the data
The code below will fit a model to a dataset using a GLM and the binomial distribution for the residuals. This is the most commonly used option for GLMs and expects the measured values to follow a logistic. This is typically used for binary data such as presence/absence, burned/unburned, etc.
TheModel=glm2(Measures~Xs,data=TheData,family=binomial) # logit (binary) summary(TheModel)
The output is similar to a linear model with the exception of a few new items.
Call:
glm2(formula = Measures ~ Xs, family = binomial)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.19011 -0.18968 0.02669 0.18966 2.25542
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -7.86152 1.78795 -4.397 1.10e-05 ***
Xs 0.15882 0.03521 4.511 6.45e-06 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 138.589 on 99 degrees of freedom
Residual deviance: 41.339 on 98 degrees of freedom
AIC: 45.339
Number of Fisher Scoring iterations: 7
Note that at the bottom is the AIC. This and the model itself, are the two key pieces of information for model selection. The "Null deviance" is effectively the "-2ln(L)" portion of the AIC for a "Null" model and the "Residual deviance" is the same calculation for the fitted model (i.e. the residual deviance should be less than the Null deviance. The "Fisher Scoring" is the method used to find the maximum likelihood and is not critical for model selection.
The standard error of the ceofficient represents how well the coeficient has been estimated (http://tinyurl.com/j5ccvgo). The z value is the regression coeficient divided by the standard error. If the z-value is large (>2), then the coeficient matters (http://tinyurl.com/hxexbtg). The Pr(>|z|) is like a p-value.
We can view the fitted values and plot them with:
fitted(TheModel)
plot(fitted(TheModel))
Note that there are two functions that will create a prediction for a GLM, "predict()" and "fitted()". Sources on the web indicate that predict() does not include the "link" function so it should not be compared with the original data. However, in my experience, predict() does overlay the original data properly so it must be applying the link function and fitted() will only predict against the original model values. If you want to predict against a new set of predictors (to make a map, for instance), you'll need to use predict. Note that the "type="response"" parameter is also required.
Xs=as.vector(array(1:100)) # create a vector with the full range of x values NewData=data.frame(Xs) # put this into a dataframe for prediction (names must match the model) ThePrediction=predict(TheModel,newdata=NewData,type="response") # create the prediction
Note that GLM is much pickier about it's inputs than most R functions. You may receive errors for having too few points or too many. Also, if it cannot find a reasonable result, it can also provide errors.
Start by plotting your prediction against the original data and you should have something like the following:
plot(TheData$Xs,TheData$Measures) # plot the original points points(Xs,ThePrediction,col=2,pch="+") # plot the prediction
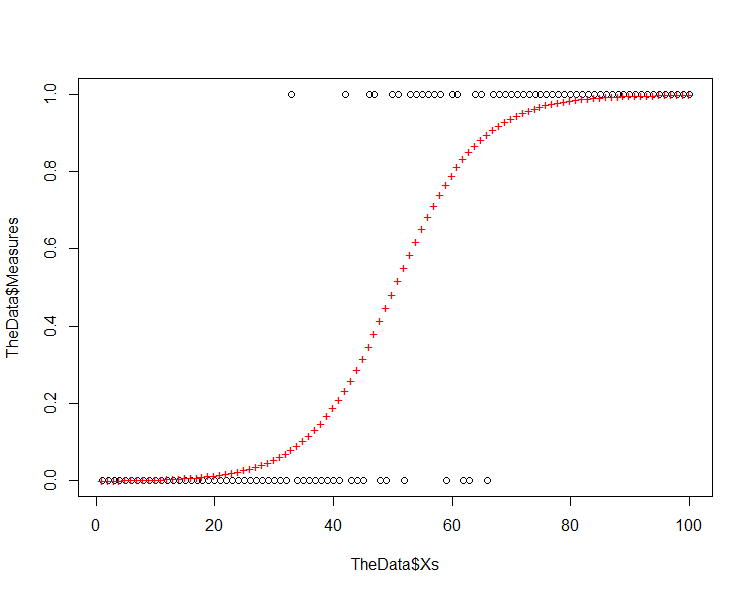
Note that the residuals increase as we move from the response values of 0 and 1 toward 0.5. This is inherent in a model where we are using a logistic equation to model a binary phenomenon.
Now, run the model plots again to produce four graphs that can be used to interpret the model:
plot(TheModel)
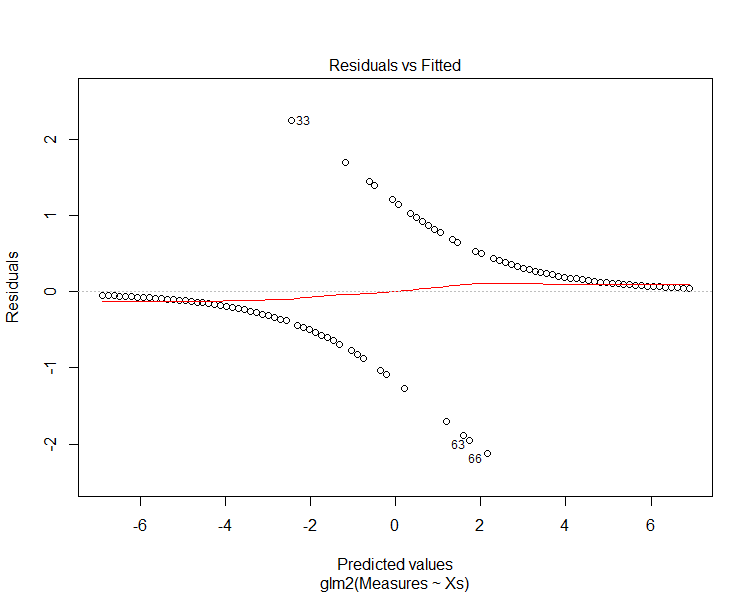
The "residuals vs. fitted" plot shows the residuals on the y-axis and the fitted values (y values from the samples) on the x-axis. Another way to think of this is that the x-axis shows the predicted value along the trend line and the y-axis shows the difference between this value and the sample value (i.e. the residual).
Note that the predicted values diverge from the prediction near the center of the graph. Examining the previous chart explains why this is happening. These plots are intended for linear models and can be misleading for GLMs.
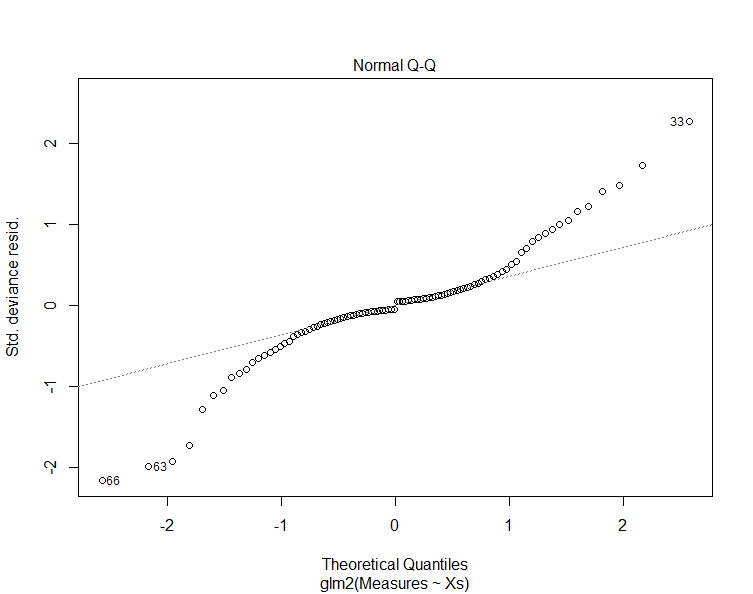
The next graph shows a Normal Q-Q plot. This plot breaks the original data into "quantiles" or buckets where each bucket as about the same number of data points. Then the mean value of each bucket is plotted for the original data against what we would expect from the model. The dashed line shows the expected value. Similar to the Resiual vs. Fitted plot, this plot is not an effective way of evaluating residuals for logistic data but will be of use for other continous data sets.
We can obtain the residuals and histogram them as below:
residuals(TheModel)
hist(residuals(TheModel))This shows how the residuals are not normally distributed and actuall form a bimodal distribution.
Below are some of the other link functions provided by the glm2() function. Try them with your data and evaluate the AIC values against the response curves provided.
TheModel=glm2(Measures~Xs,data=TheData,family=gaussian) # identity (eg. linear) TheModel=glm2(Measures~Xs,data=TheData,family=poisson) # log (eg. counts) TheModel=glm2(Measures~Xs,data=TheData,family=binomial) # logit (eg. binary) TheModel=glm2(Measures~Xs,data=TheData,family=Gamma) # inverse (eg. distances)
Note that the AIC values are not comparable across the methods for GLM. They are only valid for comparison within one method and with the same data set. We'll chat more on this later.
The function used above to create the synthetic data has two parameters. The first indicates the number of data points to generate and the second the amount of randomness or "noise" to put into the model. Try some different values for these parameters including 0 for the randomness. Note that the GLM function cannot always create a valid model.
If your data does not contain binary data (0s and 1s), you'll want to convert it to binary data. If you do not have one available, I recommend using the Count data for California dataset on the top of the GSP 470/570 web page. This dataset contains counts for Doug-Fir trees in all the FIA plots in California.
Follow the instructions in step 1 of the Creating Predictive Maps with R page and then create a GLM. Then, use steps 3 through 5 on the same page to create a predicted surface for your model.
Example
Below is a worked example that includes converting a count to presence/absence.
library(glm2)
############################################################################
# Creates a data frame with Xs ranging from 1 to the number of entries
# and "Measures" with 1/2 set to 0 and 1/2 set to 1. The lower have of
# the X values have measures at 0.
# ProportionRandom - amount of uniform randomness to add
############################################################################
TheData = read.csv("C:\\Users\\jg2345\\Desktop\\GSP 570\\Lab4 GLM\\Points from Raster2.csv")
# Remove any NA (null) values
TheData=na.omit(TheData)
# Convert an attribute (vector column) to numeric
BooleanValues=TheData$Count>0
Present=as.numeric(BooleanValues)
TheData=data.frame(TheData,Present) # add the numeric (0s and 1s) into the dataframe
TheData=na.omit(TheData) # make sure we remove any non-numberic values that might have been produced
# Plot the data
TheData$Percip=as.numeric(TheData$Value)
plot(TheData$Percip,TheData$Present) # plot the data
# Create the GLM
TheModel=glm2(Present~Percip,data=TheData,family=binomial) # logit (binary)
summary(TheModel)
# Predict values based on the model
ThePrediction=predict(TheModel,newdata=TheData,type="response") # create the prediction
# Plot the data and the predicted values
plot(TheData$Percip,TheData$Present) # plot the data
points(TheData$Percip,ThePrediction,col=2,pch="+") # plot the prediction
# add the prediction to the existing dataframe
FinalData=data.frame(TheData,ThePrediction)
plot(FinalData$Percip,FinalData$ThePrediction)
# Save the prediction to a new file
write.csv(FinalData, "C:/Temp/ModelOutput.csv")
There are some excellent labs available for R from MSU. Go through Lab 4 up to "Examples with the Use of R". The data for this lab is available in Lab 1. It is in an "R" file but needs to be loaded as a table as shown in the lab and there are some data quality issues that need to be addressed (I've made notes in a custom copy of the lab). It is also worthwhile to go through Lab 1 as practice.
© Copyright 2018 HSU - All rights reserved.