Computers encode numbers in binary (base 2) and have a limited number of "bits" to record both integer and floating-point values.
Note: These examples were originally created for Python 2.X. With Python 3.x, all the integer variables are of "infinite" precision and the floats are always double precision. Also, equations such as 1/3 will automatically be converted to floating-point.
The "format()" function will convert anything you send it into text (i.e. a 'string') so you can concatenate it with another string and print it out. This allows us to write out numbers with strings before and after them. Try the following:
x=12345
print("The value of x is "+format(x))
If we did not use "format()" we would get an error because our vairable x does not contain text, it contains a numeric value.
The "type()" function will return a value that describes the type of a variable (i.e. int, long, float, etc.). Try the following to see what "type" the x and y variables are.
x=123
TheTypeOfX=type(x)
print("The type of x is "+format(TheTypeOfX))
y=2.5
TheTypeOfY=type(y)
print("The type of y is "+format(TheTypeOfY))
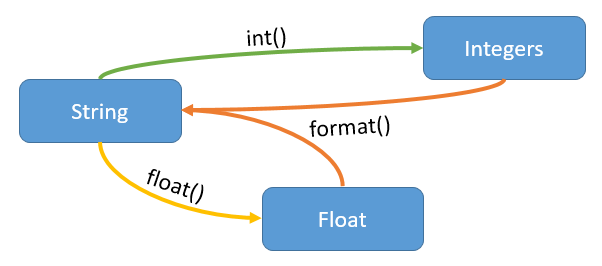
The figure below shows how to convert from numbers to strings and back again.
In most languages you have to watch the size of your integer values to make sure they don't go beyond the possible bounds of the value. However, in Python you don't really have to worry about this. Python will default to an "integer" value which can be between about -2 billion to 2 billion. When your numbers go over that amount Python will convert the variable automatically to an integer that can be of virtually any size (until it runs out of memory). Try the following code to see a demonstration. Feel free to change the size of the loop to see just how big the numbers can be!
x=pow(2,30) # start at 2^30th an integer (32 bits)
count=0
while (count<3):
print("x="+format(x)+" Type="+format(type(x)))
x=x*2 # when x goes from 2^30th to 2^31st the type will change to long (64 bits)
count+=1
Floating point numbers in Python are represented by 64-bit floating point numbers. These numbers can be from -2^1023 to 2^1023 which are really big numbers so you basically don't have to worry about floating point values either!
x=float(pow(2,1023)) # start with 2^1023 (a really big number)
count=0
while (count<2):
print("x="+format(x)+" Type="+format(type(x)))
x=x*2 # the number will go to infinite when at 2^1024 because this is too big for a float
count+=1
When you define a variable it will automatically become an integer unless it contains a fractional portion, then it will be defined as a float. When the number becomes too large for a 64-bit float, it will convert to infinite or "inf". You can test for infinity using the math packages "isinf(x)" function.
At rare times a floating point value can also contain a value that is "not a number" or "nan". This can happen if you divide 0 by infinity. You can test for "nan" using the math packages "isnan(x)" function.
Historical Note
Floating point calculations used to be very slow and we used to have much smaller amounts of memory. Today, we really don't have to worry about this.
Enter and run the following code:
Value=1/3 print(Value)
In previous version of Python (and other languages), the result would have been 0 because 1/3=0.33333 but the arithmetic would be done with integer numbers where the numbers after the decimal are ignored. Python 3.x automatically performs floating point arithmetic when needed. However, I still recommend using 1.0/3.0 as it is a good practice to remember where floating point arithmetric is needed.
Computers store numbers in binary (base 2). This means that they can represent integer values precisely but they cannot represent floating point values exactly as they are in decimal. Try the following:
Value=1.0/3.0
print("17 digits: {0:.17}".format(Value))
Notice that the 1/3 value does not extend indefinitely as it should and it ends with a "1". This is because this is the best that a computer can do with the 64-bit floating point values (48-bit for the mantissa or significant digits).
Note that the code above uses special formatting to print out the number of digits to 17 places. Don't worry about this yet, just copy the code.
The floating point values in Python allow a little over 15 digits of precision. This allows for large numbers but there are times when you manipulate floating point values and then find they are wrong. Try the following:
Value=1.0/3.0
print("17 digits?: {0:.17}".format((Value-0.333333333333333)*1000000000000000))
Notice that you have lost precision by subtracting a value that is close to the current value.
Python represents large floating point numbers with scientific notation. This means the values can have the form:
| Decimal Value | Scientific Notation | Python's Notation |
| 0.0 | 0.0 x 10^0 | 0.0e0 |
| 10.0 | 1.0 x 10^1 | 1.0e1 |
| 100.0 | 1.0 x 10^2 | 1.0e2 |
| 1,000,000.0 | 1.0 x 10^6 | 1.0e6 |
| 0.1 | 1.0 x 10^-1 | 1.0e-1 |
| 0.01 | 1.0 x 10^-2 | 1.0e-2 |
| 0.0000001 | 1.0 x 10^-6 | 1.0e-6 |
Try putting the values from the "Python Notation" column into a variable and see what the value looks like stored in "Stack Data". You'll see that the scientific notation is only used when the values are greater than 10,000 in magnitude.
Python Documentation: Floating Point Arithmetic: Issues and Limitations
Article: Perils of Floating-Point
© Copyright 2018 HSU - All rights reserved.