
Fortunately, alternative inferential statistics have been developed which eliminate (or at least finesse) these problems. The first technique we will explore is "Generalized Linear Models", specifically techniques known as "logistic regression" and "poisson regression."
Suppose we had two vectors:
demo <- c(0,0,0,0,1,0,1,1,1,1) x <- 1:10
plot(demo)

Suppose we try fitting a linear regression through these data.
demo.lm <- lm(demo~x) summary(demo.lm)
Call:
lm(formula = demo ~ x)
Residuals:
Min 1Q Median 3Q Max
-5.697e-01 -1.455e-01 -3.469e-18 1.455e-01 5.697e-01
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.26667 0.22874 -1.166 0.27728
x 0.13939 0.03687 3.781 0.00538 **
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Residual standard error: 0.3348 on 8 degrees of freedom
Multiple R-Squared: 0.6412, Adjusted R-squared: 0.5964
F-statistic: 14.3 on 1 and 8 DF, p-value: 0.005379
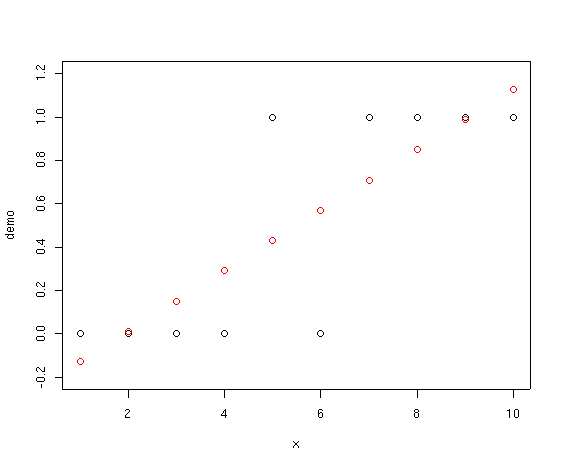
Notice how the fitted points start below 0 and slant upward past 1.0. If we
interpret these values as probabilities that species
Actually, there are two primary problems:
Alternatively, we can fit a generalized linear model that models the log of the
odds (called the logit) rather than the probability, and finesse both problems
simultaneously. If we fit a GLM as follows
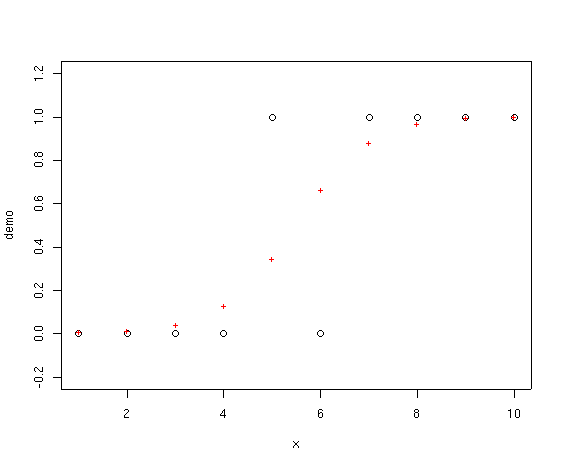
The red crosses represent the fitted values from the GLM. Notice how they never
go below 0.0 or above 1.0. In addition, the family=binomial
specification in the glm() function specifies a logistic regression
and makes sure that the fitting
function knows that the variance is proportional to the fitted value times 1
minus the
fitted value, rather
than constant.
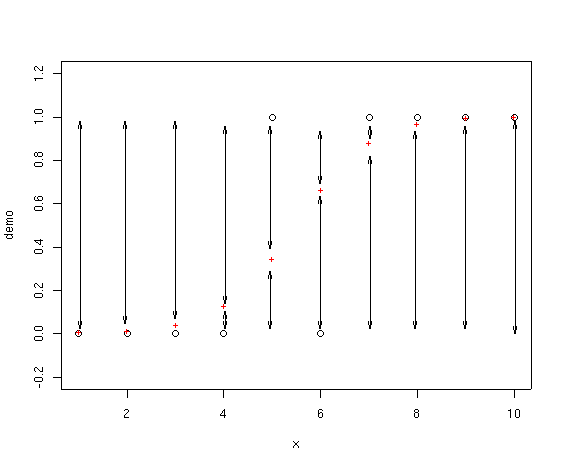
OK, so where does deviance enter in? Deviance is calculated as -2 * the
log-likelihood. In a logistic regression you can visualize the deviance as
lines drawn from the fitted point to 0 and 1, as shown below.
We take the length of each arrow and multiply that times the log of that
length and add to the same calculation for the other arrow for that point.
Finally, take -2 * the sum of all those values. If you look at the first
point, for example, the fitted value is almost exactly on top of the
actual value, so the length of one of the arrows is almost zero (and in fact not
shown on the drawing as they are too small to draw). For this point, the
deviance is very small. In fact
What's the most deviance a single point can contribute? Well, let's
look at the distribution for deviance for all probabilities between 0 and 1.
Notice how the curve is uni-modal, symmetric, and achieves its maximum value at
0.5. Notice too how probabilities greater than 0.2 and less than 0.8 have deviance
greater than 1. The maximum deviance for a single point in a logistic regression
is for probability = 0.5, where it reaches 1.386294.
Complete this section using data we extracted from the FIA database so that you can create a predicted surface. Feel free to also complete it with the Bryce Canyon data if desired.
First, get into the appropriate directory for the Bryce data, and start R.
Then, remember to attach both site and
veg.
To model the presence/absence of Berberis as a function of elevation, we use:
bere1.glm<-glm evaluates to "store the result of the generalized linear
model
in an object called 'bere1.glm'." Any object name could be used, but
"variable.glm"
is concise and self-explanatory. The number 1 is in anticipation of fitting
more models later.
berrep>0 evaluates to a logical, 0 (absent) or 1 (true), and ~
elev evaluates to "as a function of elevation." The family =
binomial tells R to perform logistic regression, as opposed to other
forms of GLM.
R calls the estimated probabilities "fitted values", and we
can use the fitted function to extract the probabilities from our GLM
object (bere1.glm). To see a graphical representation of the fitted model, do
Notice how the fitted curve is a smooth sigmoidal curve. The logistic
regression is linear in the logit, but when back transformed from the
logit to probabilities, it's sigmoidal. This is a good start, but we originally
assumed that the presence/absence of Berberis was a function of both
elevation and aspect. In addition, following conventional ecological theory we
might assume that the probability exhibits a unimodal response to environment.
To get a smooth unimodal response is simple. Just as a linear logistic
regression is sigmoidal when back transformed to probability, a quadratic
logistic regression is unimodal symmetric when back transformed to
probabilities. Accordingly, let's fit a model that is quadratic for elevation
and aspect value. We use:
~elev+I(elev^2)+av+I(av^2) evaluates to "as a function of elevation, elevation squared,
aspect value, and aspect value squared." The I(elev^2) tells R
that "I really do mean elevation squared" so that it doesn't attempt to
interpret the ^2 as an R formula operator. If you forget and
type elev+elev^2 R will mis-interpret your intent.
All together, bere2.glm<-glm(berrep>0~elev+I(elev^2)+av+I(av^2),family=binomial) models
the probability of the presence of Berberis as a unimodal function of elevation and
aspect value.
The details of the object are available with the summary function.
The output includes a Z statistic
(standardized normal deviate) and p value for each variable in the model, and tests the
hypothesis that the true value of each coefficient is 0. As you can determine
from the output, it appears that elev and I(elev^2) are
significantly different from 0, and the intercept is marginal.
While glm models do not have quite the same properties as
ordinary least squares (e.g. deviance instead of variance), you can still
get good indications about the performance of the model. Analogous to
R^2, 1-(residual deviance/null deviance) is a good indicator of overall
model fit. E.g.
The test being performed assumes
that the difference in deviance (See Deviance column) attributed to a
particular variable is distributed as Chi-square with the number of degrees of
freedom attributed to that variable (See Df column). E.g., the
elev variable achieves a reduction in deviance of 66.247 at a cost of 1
degree of freedom; the associated probability of that much reduction by chance
(Type I error) is essentially 0. It is important to realize that this table
uses the variables in the order given in the equation, and that each variable is
tested against the residual deviance after earlier variables (including the
intercept) have been taken into account.
The indication is that elevation is very important, and that the quadratic
term is also statistically significant. Neither av nor I(av^2) is significant,
at least after accounting for elevation.
For nested models (where a simpler model is a formal subset of the more complex
model) it is also possible to compare glms with the anova function as follows:
Alternatively, we can compare the AIC values for the two models with the
AIC() function. Here, we choose the model with the smaller AIC as
superior. The output is much more terse, and we have to remember which terms
are in each model.
The analysis suggests that addition of av and av^2 is not a significant
improvement, as we determined before.
So, how good is the model? For the time being (and for the sake of
demonstration), we're going to stick with our full model even though we don't
believe av matters. We'll delete it later and see the results.
Our pseudo-R^2 of 0.34 suggests that the model is
not great, but plant species are often difficult to model well, and we've just
started. To evaluate the model more fully, let's look at graphic output.
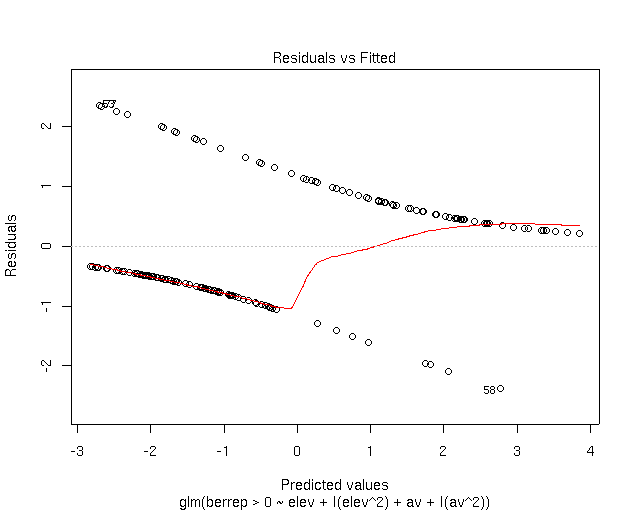
As you can see, the residuals occur in two curves; the upper one corresponds to
plots where Berberis occurs, and the lower to absence sites. The X and axes
are in logits (log of the odds), rather than probabilities, because that's the
scale that the model (and thus the residuals) is fit on.
Note that
the density of points is higher on the upper curve for fitted values
> 0.75, with residuals approaching 0. Similarly, the density of points
on the lower curve is higher at fitted values
< 0.3, again with residuals near 0. So, sites where Berberis is
present mostly have high fitted values, meaning that the model would predict
Berberis there. Unfortunately, Berberis also occurs on sites with
fitted values approaching 0, meaning that Berberis is definitely not
predicted at those sites; those are errors. Mostly, however, where Berberis is
absent, we predict absence.
The second plot shows the ordered residuals compared to a normal distribution.
If the residuals are approximately normally distributed we can have more faith
in the robustness of the model. In this case, our extreme residuals are more
extreme than a normal distribution, but that's not uncommon for GLM models.
As an alternative, we can calculate the fraction (or equivalently, percent) of plots
correctly predicted with the table function. Since R refers to
the estimated probabilities as fitted values, we can use the fitted
function to extract the fitted values and do the following:
That's all well and good, but what does our model really look like? Well, the
current model is multi-dimensional for elev and av, so it's
problematic to look at directly.
In this case we can look at the model
one dimension at a time.
Notice how the points make a fairly smooth curve as elevation increases; this
is the effect due to elevation. Notice also that there is a small vertical
distribution of points at any given elevation; this is the effect due to aspect
value. Notice also that the thickness of the band due to aspect value is about
0.2 at its maximum, while the amplitude of the elevation curve goes from about
0.1 to 1.0. This is a crude estimate of "effect size", where elevation has more
than 5 times the effect as aspect value on the predicted value. We can make
more precise estimates later, but graphic intuition is always nice, and we don't
have to learn any more R to see it. The points command above
colors those plots where Berberis actually occurs, so we again get a
sense of how well the model is doing.
As we noted before, the av and I(av^2) variables are not
contributing significantly to the fit. If we look at the model without them, we get:
Notice how the scatter due to av is now gone, and we get a clear picture of
the relationship of the probability of Berberis to elevation. Notice too
that the curve actually goes up slightly at lower elevations; this is
unexpected and probably ecologically improbable given what we know about species
response to environment. While it first appeared that the GLM was successful in
fitting a modal response model to the elevation data, what we actually observe is a
truncated portion of an inverted modal curve. If you go back and look at the
coefficients fit by the model, you see:
In fact, converted to a simple
test, the simple GLM has equal prediction accuracy (0.85).
As another example of nested calls,
we can plot the linear model without storing it as follows:
The analysis added soil depth to the existing model. The notation
update(bere.glm,.~.+depth means update model bere.glm, use the
same formula, but add depth. The na.action=na.omit means omit
cases where soil depth is unknown. Unfortunately, several plots in the data set
don't have soil data.
As you should recall from Lab 2, soil depth and elevation were not independent,
with deeper soils generally occurring at lower elevations. This last model
suggests that soil depth is significant, even after accounting for elevation.
We actually observe slightly higher deviance reduction due to elevation than
before, but this is due to dropping those plots where soil depth is unknown, not
to a change in the effect of elevation.
Variables can be dropped as well, as for example:
Note, however, that I had to use the I(av^2) instead of the simpler
av^2 to get the correct result.
Generalized linear models are an enormously powerful tool for the analysis of
the distribution of plant species along environmental gradients. A
variant of this approach using principles of parsimony has been advocated by
Huisman, Olff and Fresco (1993). They proposed testing a series of
increasingly more complicated models from a flat null model to a skewed
(non-symmetric) curve for individual species. However, their models are not
easily fit by the maximum likelihood methods of GLM, and require non-linear
regression by least squares (although see the HOF
models of Jari Oksanen for a maximum likelihood approach). Note: This secton uses abundance from 0 to 100% and is optional for GSP 570. In all the above regressions, we have modeled the probability of the presence of
Berberis repens. If we want to model the expected abundance of Berberis repens
we can still use GLM, but we need to specify the model slightly differently. As you will recall,
the two elements of GLM were to finesse the boundedness problem of the dependent variable, and to
use the appropriate variance for the estimated values. If we want to model expected abundance in percent cover,
it is again bounded at the lower limit at 0.0, but is now bounded at the upper end at 100.0.
This is actually a tricky model to fit. If none of the observed or expected values actually
approach 100.0, we can treat the distribution as bounded at 0 on the low end,
and unbounded on the upper. In this case, the best choice might be a Poisson
distribution, where we treat the percent cover as equivalent to numbers of
individuals, ramets, or modules.
Back in Lab 1 we created a dataframe called cover which had the cover
class midpoints instead of cover codes. Using this, let's model the expected
abundance of Berberis repens. The most important change we will make in
the function call is to specify a new family. For a Poisson
distribution the variance is proportional to the mean, and we can specify that
with family='poisson' in our function call, instead of
family='binomial'. A second, trivial change is to round the percent
cover to integer values, as a Poisson distribution expects counts. An
alternative is to use ceiling() instead of round, which converts real
numbers to the smallest integer that is larger than the number. In our case,
round(0.5) = 0 while ceiling(0.5) = 1.
Often the distributions of plant species are difficult to model due to extreme
values in the distribution. As an example of a contrast, let's try
Arctostaphylos patula.
ter Braak, C.J.F. and C.W.N. Looman. 1995. Regression. Pages 39-77 IN
R.H.G. Jongman, C.J.F. ter Braak, and O.F.R. Van Tongeren. (eds.) Data
analysis in community and landscape ecology. Cambridge University Press.
demo.glm <- glm(demo~x,family=binomial)
plot(x,demo,ylim=c(-0.2,1.2))
points(x,fitted(demo.glm),col=2,pch="+")
1 2 3 4 5 6
0.002850596 0.010397540 0.037179991 0.124285645 0.342804967 0.657195033
7 8 9 10
0.875714355 0.962820009 0.989602460 0.997149404
q <- seq(0.0,1.0,0.05)
plot(q,-2*(q*log(q)+(1-q)*log(1-q)))

Examples with the Use of R

plot(elev,fitted(bere1.glm),xlab='Elevation',
ylab='Probability of Occurrence')

Call:
glm(formula = berrep > 0 ~ elev + I(elev^2) + av + I(av^2),
family = binomial)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.3801 -0.7023 -0.4327 0.5832 2.3540
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 7.831e+01 4.016e+01 1.950 0.0512 .
elev -2.324e-02 1.039e-02 -2.236 0.0254 *
I(elev^2) 1.665e-06 6.695e-07 2.487 0.0129 *
av 4.385e+00 2.610e+00 1.680 0.0929 .
I(av^2) -4.447e+00 2.471e+00 -1.799 0.0719 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 218.19 on 159 degrees of freedom
Residual deviance: 143.19 on 155 degrees of freedom
AIC: 153.19
Number of Fisher Scoring iterations: 5
Analysis of Deviance Table
Model: binomial, link: logit
Response: berrep > 0
Terms added sequentially (first to last)
Df Deviance Resid. Df Resid. Dev P(>|Chi|)
NULL 159 218.193
elev 1 66.247 158 151.947 3.979e-16
I(elev^2) 1 5.320 157 146.627 0.021
av 1 0.090 156 146.537 0.765
I(av^2) 1 3.349 155 143.188 0.067
bere3.glm<-glm(berrep>0~elev+I(elev^2),family=binomial)
anova(bere3.glm,bere2.glm,test="Chi")
Analysis of Deviance Table
Model 1: berrep > 0 ~ elev + I(elev^2)
Model 2: berrep > 0 ~ elev + I(elev^2) + av + I(av^2)
Resid. Df Resid. Dev Df Deviance P(>|Chi|)
1 157 146.627
2 155 143.188 2 3.439 0.179
df AIC
bere2.glm 5 153.1878
bere3.glm 3 152.6268

FALSE TRUE
FALSE 83 9
TRUE 15 53
plot(elev,fitted(bere2.glm))
points(elev[berrep>0],fitted(bere2.glm)[berrep>0],col=2)


elev -2.323e-02 1.030e-02 -2.256 0.0241 *
I(elev^2) 1.664e-06 6.631e-07 2.510 0.0121 *
Analysis of Deviance Table
Response: berrep > 0
Resid. Df Resid. Dev Df Deviance P(>|Chi|)
elev + I(elev^2) 157 146.627
elev 158 151.947 -1 -5.320 0.021
df AIC
bere3.glm 3 152.6268
glm(berrep > 0 ~ elev, family = binomial) 2 155.9469
FALSE TRUE
FALSE 83 9
TRUE 15 53
bere4.glm<-update(bere2.glm,.~.+depth,na.action=na.omit)
anova(bere4.glm,test="Chi")
Analysis of Deviance Table
Model: binomial, link: logit
Response: berrep > 0
Terms added sequentially (first to last)
Df Deviance Resid. Df Resid. Dev P(>|Chi|)
NULL 144 197.961
elev 1 69.702 143 128.258 6.896e-17
I(elev^2) 1 2.677 142 125.581 0.102
av 1 0.080 141 125.502 0.778
I(av^2) 1 7.592 140 117.910 0.006
depth 1 12.422 139 105.488 4.243e-04
bere5.glm<-update(bere2.glm,.~.-av-I(av^2))
summary(bere5.glm)
Call:
glm(formula = berrep > 0 ~ elev + I(elev^2), family = binomial)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.5304 -0.6914 -0.4661 0.5889 2.1420
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 7.310e+01 3.979e+01 1.837 0.0662 .
elev -2.167e-02 1.027e-02 -2.110 0.0349 *
I(elev^2) 1.560e-06 6.613e-07 2.359 0.0183 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 218.19 on 159 degrees of freedom
Residual deviance: 146.63 on 157 degrees of freedom
AIC: 152.63
Number of Fisher Scoring iterations: 4
Poisson Regression
bere6.glm <- glm(round(cover$berrep) ~ elev + I(elev^2),family='poisson')
summary(bere6.glm)
Call:
glm(formula = round(cover$berrep) ~ elev + I(elev^2), family = "poisson")
Deviance Residuals:
Min 1Q Median 3Q Max
-2.773616 -0.548849 -0.119568 -0.006365 10.734024
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.948e+02 1.063e+02 -1.833 0.0668 .
elev 4.124e-02 2.484e-02 1.660 0.0969 .
I(elev^2) -2.153e-06 1.451e-06 -1.484 0.1379
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 504.37 on 159 degrees of freedom
Residual deviance: 266.05 on 157 degrees of freedom
AIC: 337.36
Number of Fisher Scoring iterations: 7
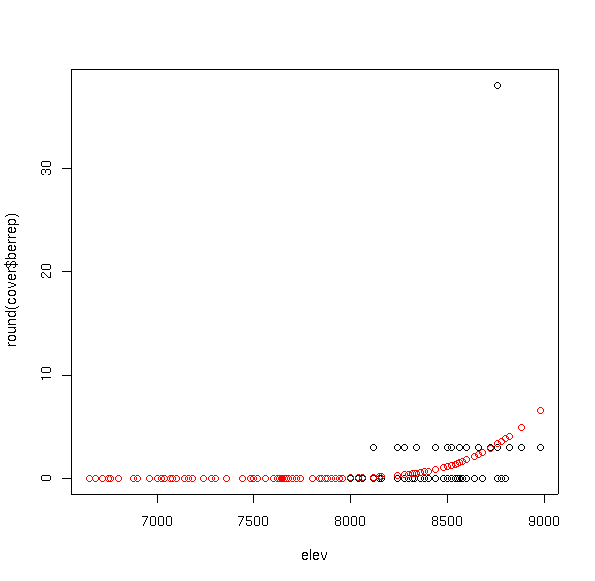
plot(elev,round(cover$berrep))
points(elev,fitted(bere6.glm),col=2)
arpa.glm <- glm(round(cover$arcpat) ~ elev + I(elev^2),family='poisson')
summary(arpa.glm)
Call:
glm(formula = round(cover$arcpat) ~ elev + I(elev^2), family = "poisson")
Deviance Residuals:
Min 1Q Median 3Q Max
-6.529 -5.724 -4.632 2.722 13.888
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -4.657e+01 4.590e+00 -10.147 <2e-16 ***
elev 1.168e-02 1.152e-03 10.136 <2e-16 ***
I(elev^2) -6.871e-07 7.214e-08 -9.526 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 6018.6 on 159 degrees of freedom
Residual deviance: 5479.2 on 157 degrees of freedom
AIC: 5774.6
Number of Fisher Scoring iterations: 7
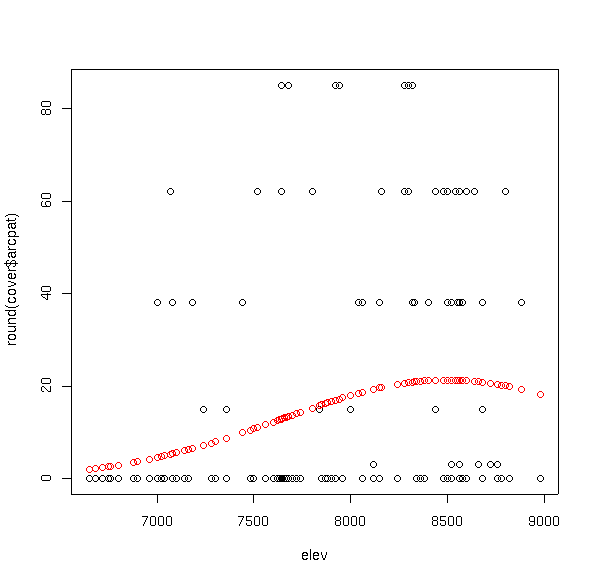
plot(elev,round(cover$arcpat))
points(elev,fitted(arpa.glm),col=2)
References
Huisman, J., H. Olff, and L.F.M. Fresco. 1993. A hierarchical set of models for
species response analysis. Journal of Vegetation Science, 4, 37-46.